. Трикутники ВСK і CAN гострокутні

Страрегія дослідженя

Хлівнюк Аліна

Захист роботи

\

II.Ортоцентр гострокутного трикутника є внутрішньою точкою трикутника

CD – спільна висота трикутників АCN  і BCK

Якщо існує спільний ортоцентр вказаних трикутників, то він обов’язково  належить СD

З’ясуємо, чи існують такі трикутники

Опустимо перпендикуляр с т К на СB

О точка перетину КЕ і СD

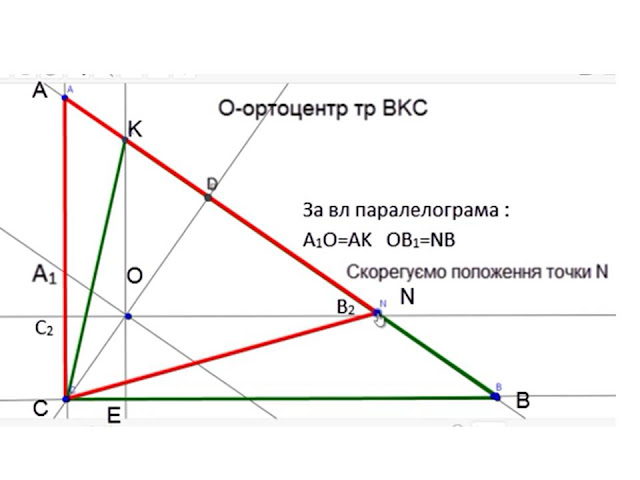
O-ортоцентр трикутника BСK і він повинен бути ортоцентром трикутника АСN

Проведемо  A₁B₁ II  AB. Проведемо   С₂B₂ II  СB

За властивістю паралелограма :

                                                                                                                                              А₁О=AK 

  OB₁=NB 

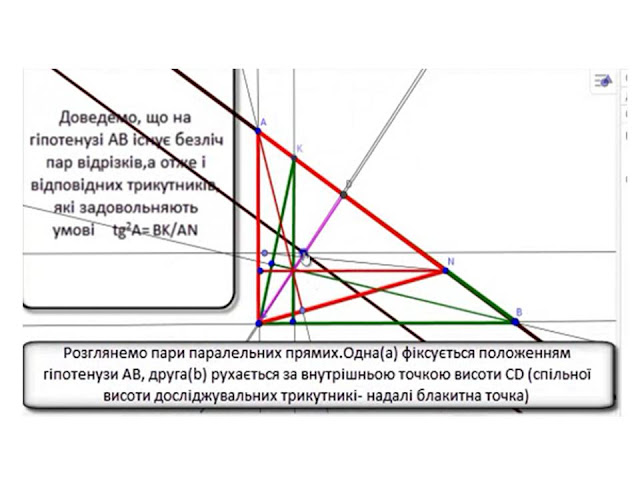
Відслідкуємо динаміку руху утвореної системи прямих

Оскільки процес руху блакитної точки перетину прямої b, висоти CD, и перпендикуляра h внутрішньої точки СD неперервний, то розглянуті всі можливі випадки для гострокутних трикутників А_iCN_i і  B_ICK_i.

tg²А= p_i/ m_i ;    K_iB_i=m_i;        A_iN_i=p_i         0 < p_i  <  AD

Причому:      0 < p_i  < AD        0 < mi< BD 

   tg² А= m_i/p_i=B_i K_i/A_i N_i= BK/A N

 для кожного  фіксованого і-тoго трикутника  A_iCB_i   Відповідні пари відрізків K_iB_i=m_i;        A_iN_i=p_i         лежать на гіпотенузі  AB. Висота СD є множиною спільних ортоцентрів трикутників А_iCN_i і  B_ICK_i

Що і потрібно було довести